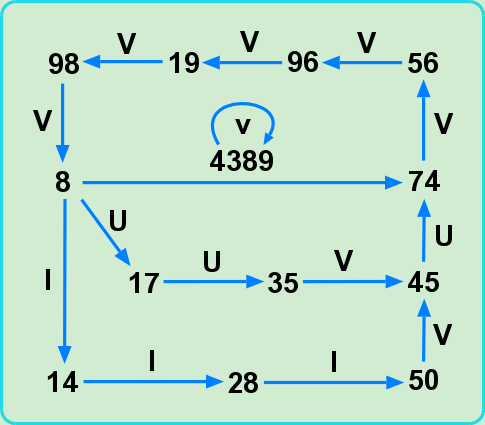
Symmetric view of 8 and 74

Chapters 8 and 74 share several interesting properties. First, we notice that the sum of the digits of the verses of chapters from 1 to 8 is 74:
(7) + (2 + 8 + 6) + ... + (2 + 0 + 6) + (7 + 5) = 74.
Also, we recall that 19 is of index 8 (see Glossary) and it only appears in chapter 74, not for counting purposes unlike other numbers, but as an abstract number.
As illustrated in the above diagram there are several paths between 8 and 74. The top portion of the figure shows a path connecting several successive intervening chapters (nodes) via their verses (V arrows). The sum of these nodes is:
74 + 56 + 96 + 19 + 98 + 8 = 351 = 13 × 27.
We recognize that 27 is of ord 13. Furthermore, 13 has 43 verses and 43 has 89 verses (Small curly V arrow). And from 8 to 74 there are 4389 verses as indicated by the long arrow. Chapter 43 is of ord 24 and 89 is the 24th prime number, also 4 + 3 + 8 + 9 = 24, and chapter 24 is of ord 13.
From 43 to 89 there are 24 odd chapters with total of 874 verses! Both 874 and 4389 are divisible by 19; 874 = 19 × 46, where 46 itself is of ord 27. Additionally, 874 + 4389 = 5263 = 19 × 277, and this happens to be the number of verses from 2:1 to 68:1, the first and last declarations, respectively, (Appendix 1). We note that 874 is the smallest integer with digit-sum, 19. Also, as an interesting side-note, from 74:1 to 114:6 there are 741 verses! it is noteworthy that the counts of initialed letters from 13 to 19 add up to the same sum:
1482 + 1197 + 912 + 798 = 4389.
From the Fig. we see there are two more paths from 8 to 74 via the initialed and un-initialed intermediate nodes (UUVU and IIIVU paths). We may further break down 4389 as a sum of two: 4389 = 2051(I) + 2338(U), corresponding to initialed and un-initialed verses from 8 to 74. The two summands happen to be the grames at the end of chapters 33 and 47, respectively. G:33 contains 19 chapters with 27 total grame. With 47 having 38 verses, we may put down a simple relationship between 43, 47, 9, and their corresponding verses:
4389 + 4738 = 9127.